"Deep Reinforcement Learning From Human Preferences" Paper Explained

This paper is the work of a collaboration with Deep Mind and Open AI, improving the field of Deep Reinforcement Learning. 

The ideas discussed in this paper are also a key component in the training of GPT-4. 

RL agents need good reward functions to learn complex tasks. However, it takes work to design reward functions from scratch. 

Learning a reward function using a neural network is also proposed. Another idea is why not let a human reward the agent altogether.

This paper attempts to combine both of those two ideas. 

The method discussed in this paper is a crucial component that Open AI used in training GPT-4. 

Introduction 

Reinforcement learning is a learning paradigm in which an agent observes the environment, takes an action, and receives a reward. 

This process happens continuously in a loop. 

The agent's objective is to maximize the reward it accumulates by taking proper actions at the appropriate timestep t. 

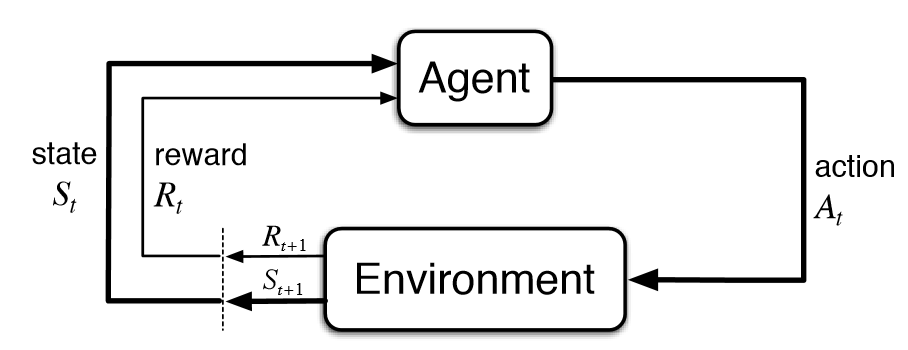
Notice that in traditional reinforcement learning, the environment gives the agent its reward.  

That means we need to design a reward function by looking at the environment at that timestep and see what amount of reward should be given to the agent. 

Designing a simple reward function that approximately captures the intended behavior is problematic in complex tasks. In most cases, this leads to the agent optimizing for the reward function without satisfying the intended preferences. 

Instead of designing a reward function, we can use a human to give out a reward by observing the environment. However, this is very expensive and time-consuming. 

Therefore we need to devise a way that uses human feedback very sparingly. 

The approach mentioned in the paper is to learn a reward function from human feedback and then optimize that reward function. This reward function is responsible for giving out rewards to the agent. The agent then optimizes its behavior to the learned reward function. 

The method proposed in the paper is beneficial in tasks where humans can recognize the desired behavior, but one that you can only demonstrate to the agent what the desired behavior is. 

For example, consider an agent doing a black flip. You know when the agent does a backflip correctly and when an agent doesn't.  
But it would be easier to do a backflip if you are an expert at doing a backflip. 

This method allows agents to be trained by non-experts. 
This method also scales to significant complex problems and claims to be economical with human feedback. 

The algorithm proposed in the paper fits a reward function to given human feedback while simultaneously training a policy to optimize the currently predicted reward function. 

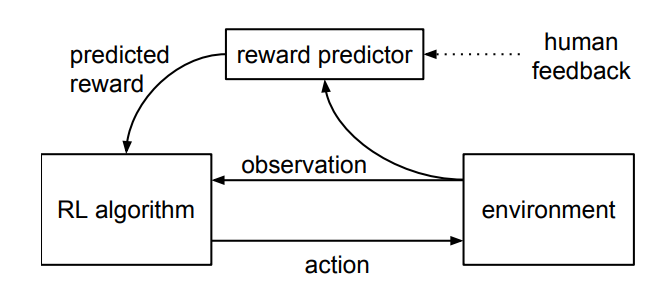
The human feedback is taken from a subject (volunteer, nonexpert), where they compare short video clips of the agent's behavior. 

The subject picks one of the video clips with the correct behavior, or if both video clips are equally bad or equally good, they can choose "cannot be decided." 

Since human feedback is taken in real-time, and the reward function changes in real-time, the agent cannot exploit the reward function since it constantly modifies (volatile). This method leads to the agent working in line with human preferences. 

Related Work 

The paper follows the same basic approach as previous works, "Active preference learning-based reinforcement learning" and "Programming by Feedback" by Akrour et al. 

A difference from previous works is that this paper uses short clips instead of whole trajectories when getting feedback from the human subject. 

This paper has two orders of magnitude more comparisons but requires considerably less human time. 

The method proposed in this paper collects and processes human feedback, following closely with previous work, "A Bayesian approach for policy learning from trajectory preference queries" by Wilson et al. 

However, Wilson's work uses "synthetic" human feedback drawn from a Bayesian model, whereas this paper uses nonexpert users. 

"Interactive learning from policy-dependent human feedback" by MalGlashan et al., "Online human training of a myoelectric prosthesis controller via actor-critic reinforcement learning" by Pilarski et al., 

"Interactively shaping agents via human reinforcement: The TAMER framework" by Knox and Stone and "Learning non-myopically from human-generated reward" by Knox are previous works focusing on human feedback-based reinforcement learning.

The above works have learning only occurring during episodes where the human trainer provides feedback (MalGlashan et al. and Pilarski et al.). However, this approach is not feasible in domains where an RL agent needs thousands of hours of trial and error to converge to an optimal policy. 

The works of Knox and Stone also learn a reward function. However, they consider much simpler settings where the desired policy can be quickly learned. 

The essential contribution of this paper is to scale human feedback up to deep reinforcement learning and to learn much more complex behaviors. 

This paper fits into the recent trend of works that were focused on scaling reward learning methods to large deep learning systems, e.g. Inverse RL (Deep inverse optimal control via policy optimization by Finn et al.), Generative adversarial imitation learning by Ho et al., Generalizing skills with semi-supervised reinforcement learning by Finn et al.

The methodology 

The paper tests their new method on the following RL training environments. 

1. Arcade Learning Environment (ALE) - For testing RL agents using Atari Games 
2. MuJoCo - For testing robotic tasks via a physics simulator 

An RL agent interacts with the environment as follows, at each timestep (\ t \), the agent receives an observation \( o_t \in O \) from the environment and then sends an action \( a_t \in A \) to the environment. 

Traditionally, the environment would provide reward signals, but a human overseer can express preferences between trajectory segments in this method rather than the environment. 

A trajectory segment is a sequence of observations and actions.

\[ \sigma = ((o_0, a_0), (o_1, a_1), ... ,(o_{k-1}, a_{k-1})) \in (O \times A)^k \]

A pair of these trajectory segments are presented to a human at any given time. The following is how we denote that the trajectory \( \sigma^1 \) is prefered over trajectory \( \sigma^2 \) by the nonexpert user. 

\[ \sigma^1 \succ \sigma^2 \]

In informal terms, the goal of the agent in the long run is to produce trajectories which are preferred by the human, while making as few queries as possible to the human, so that less time is utilized from the prespective of the human subject (nonexpert user). 

A breakdown of the process 

At each timestep, the method proposed in the paper maintains a policy and a reward function estimate. 

The policy is a function that maps observations(from the state space O) to an action (in the action space A). 

The reward function estimate maps observations and actions to a real value (scalar). 

The policy and the reward function estimator are networks that learn over time from training and experience (via updating their weights). 

The policy interacts with the environment to produce a set of trajectories (sequences of state and action pairs), and traditional reinforcement learning algorithms update the policy's parameters to maximize the reward the agent gets over time. 

Specific pairs of segments sampled from the trajectories are taken and sent to a human for comparison and feedback. 

The parameters of the reward function estimator are updated via supervised learning to fit with the comparisons made by the non-expert human user. 

All these actions mentioned above run asynchronously from one to the other without halting the overall learning process of the agent. 

The agent or the reward function estimator doesn't halt until the human subject gives feedback, and the systems run asynchronously in the background.  

The Reward Function Estimator

The following diagram below shows their reward function estimator architecture. 

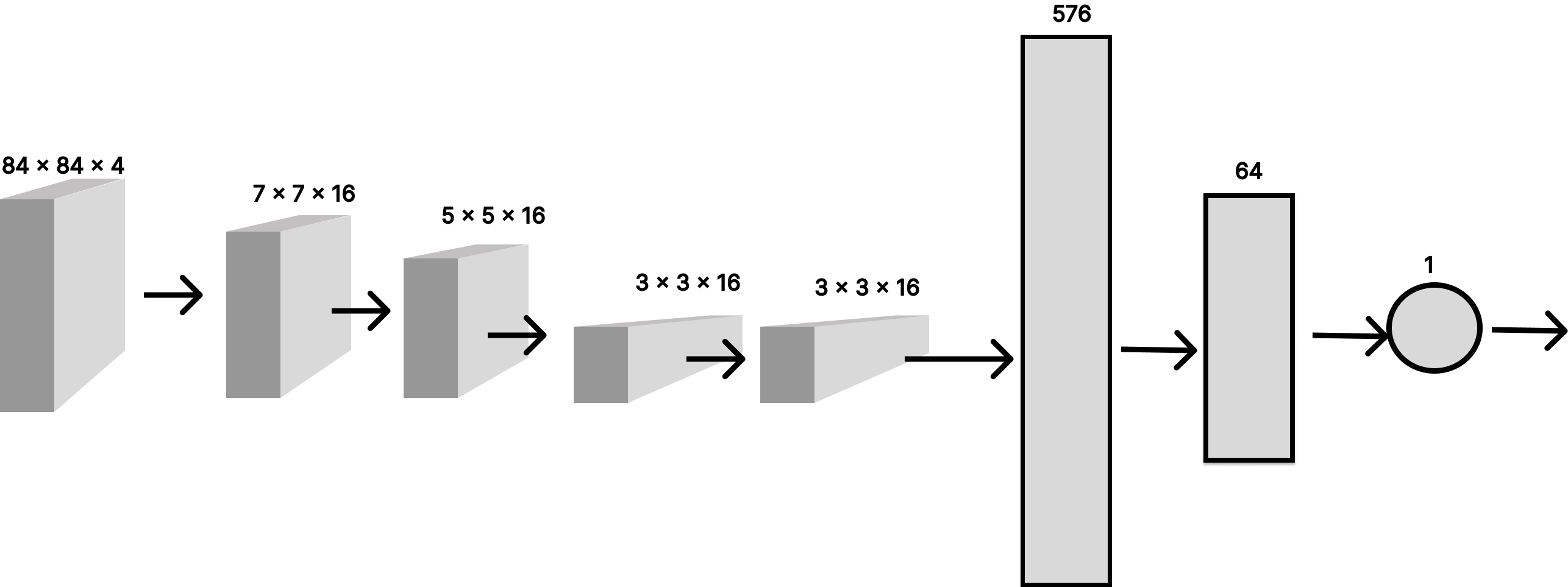
It's a convolutional neural network with multiple convolutional layers, with the input as the state, and the output is a scalar value, which is also normalized via a sigmoid function to be a value between -1 and 1. 

This reward is then given to the RL agent for any action it chooses to do. 

The human non-expert trains the reward function estimator via feedback so that for each different state, suitable rewards are given that fit in line with the human's preferences. 

Selecting queries and asking for human feedback

One of the main goals of this paper is to minimize human time and ask for as little feedback as possible when training an RL agent to do a complex task. 

The reward function estimator cannot query the human every time.  
Ideally, it should query the human subject when unsure what reward to give to a particular state and action pair.

In their method, they use several reward function estimators in an ensemble (of size 3) and consider all of the networks' predictions in the ensemble, when trying to get feedback from the non-expert human subject. 

The diagram below shows a high-level picture of how the overall process works. 

Many pairs of trajectory segments sampled from the buffer are run through the reward function estimators in the ensemble. Each network tries to predict which pair of trajectories are more likely to align with human preferences by scoring them. (A high reward predicted means the network "thinks" that the given trajectory is better, and vice versa) 

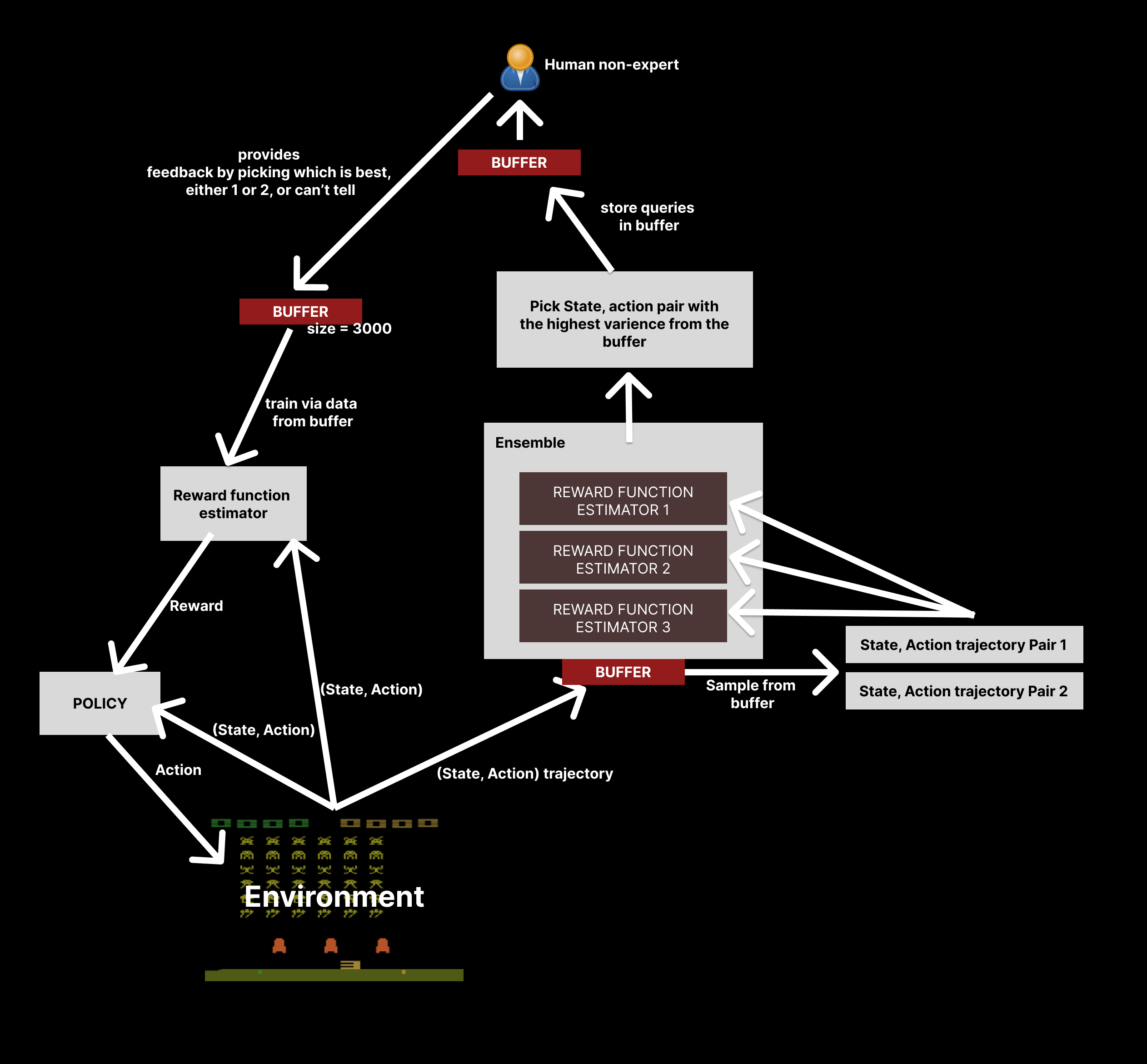
Sometimes the networks in the ensemble cannot commonly agree on which two trajectories might be better than the other, meaning those two trajectories would have high variance, the highest pair, which contains the most amount of variance, is sent to the human subject for feedback. 

The two pairs of trajectories selected forms a query, and the feedback from the human helps the reward estimator produce better rewards in the future aligned with human preferences. 

How feedback is processed 

The human subject is shown two short video clips of the pair of trajectories, lasting for about 1 or 2 seconds. 

The subject can then select whether the first clip is the best, if the second clip is the best, or if they can't decide. This response is recorded and used to construct training data for the reward estimator function to train on.

This forms a tuple  \( \left(\sigma^1, \sigma^2, \mu \right) \) where, \( \sigma^1 \) is the first trajectory, and \( \sigma^2 \) is the second trajectory, and \( \mu \) is the human preference distribution (feedback). 

The below diagram illustrates how \( \mu \) is created. 

Fitting the Reward Function 

The probability that the reward estimator function prefering trajectory \( \sigma^1 \) over \( \sigma^2 \) can be denoted by the following probability expression, 

\[\hat{P}[\sigma^1 \succ \sigma^2] = \frac{\exp \sum \hat{r} \left( o^1_t , a^1_t \right) }{\exp \sum \hat{r} \left( o^1_t , a^1_t \right) + \exp \sum \hat{r} \left( o^2_t , a^2_t \right)}\]

And the probability that the reward estimator function prefering trajectory \( \sigma^2\) over \( \sigma^1 \) can be denoted by the following probability expression, 

\[\hat{P}[\sigma^2 \succ \sigma^1] = \frac{\exp \sum \hat{r} \left( o^2_t , a^2_t \right) }{\exp \sum \hat{r} \left( o^1_t , a^1_t \right) + \exp \sum \hat{r} \left( o^2_t , a^2_t \right)}\]

Note that \( \hat{r} \) is the reward estimator function, and \( o_t \) is state, and \( a_t \) is the action taken by the agent, at timestep \( t \). 

We write the loss of the function, as a cross-entropy loss, between the difference in the trajectory preferred by the reward estimator vs. the trajectory preferred by the human subject.

Note that, \( \mu(1) \) denotes the probability that the human subject prefers trajectory \( \sigma^1 \) and \( \mu(2) \) denotes the probability that the human subject prefers trajectory \( \sigma^2 \) 

\[\text{loss}\left( \hat{r} \right) = - \sum_{\left( \sigma^1, \sigma^2, \mu \right) \in D } \mu\left(1\right)log \hat{P} \left[ \sigma^1 \succ \sigma^2 \right] + \mu\left(2\right)log \hat{P} \left[ \sigma^2 \succ \sigma^1 \right]\]

\[\text{loss}\left( \hat{r} \right) = - \sum_{\left( \sigma^1, \sigma^2, \mu \right) \in D } \mu\left(1\right)log  \frac{\exp \sum \hat{r} \left( o^1_t , a^1_t \right) }{\exp \sum \hat{r} \left( o^1_t , a^1_t \right) + \exp \sum \hat{r} \left( o^2_t , a^2_t \right)} + \mu\left(2\right)log \frac{\exp \sum \hat{r} \left( o^2_t , a^2_t \right) }{\exp \sum \hat{r} \left( o^1_t , a^1_t \right) + \exp \sum \hat{r} \left( o^2_t , a^2_t \right)}\]

Summary of results 

Novel behaviors were observed in the Atari as well as the physics environment, 

1. The Hopper robot performs a sequence of backflips. This behavior was trained using 900 queries in less than an hour. The agent learns to perform a backflip, land upright, and repeat consistently. 
2. The Half-Cheetah robot moves forward while standing on one leg. This behavior was trained using 800 queries in under an hour.
3. Keeping alongside other cars in Enduro. This was trained with roughly 1,300 queries and 4 million frames of interaction with the environment; the agent learns to stay almost exactly even with other moving cars for a substantial fraction of the episode, although it gets confused by changes in the background.

The videos of these novel behaviors can be founded here: Deep RL with Human Preferences - Google Drive

Thanks for reading!